Table Of Content
Model-Free Reinforcement Learning
- Model을 사용하지 않기 때문에 Environment에 대해서 알지 못함
- → Partially Observable Environments
- → Model Free Prediction 또는 Model Free Control 형태로 문제를 풂
- 이번 Lecutre에서 Estimate the value function of an unknown MDP 에 대해 배울 예정

Monte-Carlo Reinforcement Learning
- Monte-Carlo: 사건을 수행하면서 나오는 실제값을 통해 추정하는 것
- MC methods learn directly from episodes of experience
- MC is model-free: no knowledge of MDP transitions / rewards
- MC learns from complete episodes: no bootstrapping
- MC uses the simplest possible idea: value = mean return
- 게임을 끝까지 수행해서 게임에서 나온 결과값을 모두 더해서 평균내는 것
- Caveat: can only apply MC to episodic MDPs
- All episodes must terminate
Monte-Carlo Policy Evaluation
- Policy Evaluation == Prediction
- Value Function은 Return의 기대값
- Goal: learn vπ from episodes of experience under policy π
- S1, A1, R2, ..., Sk ~ π
- Recall that the return is the total discounted reward:
- Gt = Rt+1 + γRt+2 + ... + γT-1Rt
- Recall that the value function is the expected return
- vπ(s) = Eπ[Gt | St = s]
- Monte-Carlo policy evaluation uses empirical mean return instead of expected return
Monte-Carlo Policy Evaluation
- State 개수만큼의 칸이 있을 때, 방문할 때마다 칸의 Count를 증가시켜주고 게임이 끝날 때 얻은 Reward도 적어준다
- 한 Episode에서 방문했던 State를 또 방문할 수 있는데, 이걸 모두 방문했다고 인정해주는 게 Every-Visit
- 첫 방문한 것만 인정해주는 게 First-Visit
- Law of large number에 의해서 Fisrt-Visit 또는 Every-Visit 중 어떤 방법을 사용해도 Value Function은 동일함
- 단 Policy에 의해 모든 State를 방문한다는 가정이 있어야 함
First-Visit Monte-Carlo Policy Evaluation

- By law of large numbers: 큰 수의 법칙
Every-Visit Monte-Carlo Policy Evaluation

Blackjack Example
 |
 |
- X축: dealer가 보여주는 카드, Y축: 나의 sum 12 - 21중 어느 값인지
- Ace가 있을 때는 높고 낮음이 있는데, 50만번 학습했을 땐 사라짐 → 50만번에서 수렴
- 50만번에서 학습이 잘 되었음을 어떻게 알 수 있나?
- 50만번 학습했을 때, 평평한 그래프를 보고 나서야 비로소 수렴했음을 알 수 있다
MC > Incremental Mean
- The mean µ1, µ2, ... of a sequence x1, x2, ... can be computed incrementally
- 여러 번 수행해보고 평균 내는 것이 MC
- 앞선 방법과 동일한 결과이지만, 기존 MC에서는 각 State마다 평균 값을 저장해야함
- (즉 State를 만번 방문했으면 State 개수 * 만 개)
- Incremental Mean을 쓰면 저장하지 않고 새로운 값을 보정해주면 됨
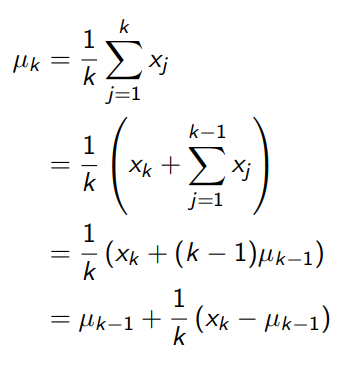
MC > Incremental Monte-Carlo Updates
- Update V(s) incrementally after episode S1, A1, R2, ..., ST
- For each state St with return Gt
- N(St) ← N(St) + 1
- V(St) ← V(St) + 1/N(St) * (Gt - V(St))
- Gt - V(St) = Error
- 즉 현재 나온 Error만큼 업데이트해주겠다
- In non-stationary problems, it can be useful to track a running mean, i.e. forget old episodes.
- V(St) ← V(St) + α (Gt - V(St))
- 1/N을 α로 고정시킬 수 있다 → 즉 예전 경험을 잊겠다
- α는 Neural Network의 Learning Rate 같은 녀석. 작게 하면 G값이 커짐(즉 과거를 잊도록)
- non-stationary problem: MDP가 조금씩 바뀌는 것을 의미
Temporal-Difference Learning
- TD methods learn directly from episodes of experience
- TD is model-free: no knowledge of MDP transitions / rewards
- TD learns from incomplete episodes, by bootstrapping
- episode가 끝나지 않아도 업데이트할 수 있다
- TD updates a guess towards a guess
- V(St)는 현재 guess인 상태
- V(St+1)로 한 스텝 더 가서 V(St)를 업데이트한다 라는 의미
MC and TD

- 현재 State St에서 Value는 V(St), 여기서 미리 t+1을 한 값을 예측하게 되면 V(St+1)
- V(St+1) 값이 V(St)보다 정확하기 때문에 그 방향으로 V를 업데이트하는 것
- 예) 차를 운전하는 중에 중앙선을 넘었고, 트럭이 차를 향해 달려오고 있다.
- 트럭이 반응속도가 좋아서 내 차를 피해갔다.
- MC에 따르면, 나는 충돌하지 안했으니까 Reward를 못받음
- TD에 따르면, 중앙선을 침범한 순간 미래 Reward가 좋지 않겠구나 하고 미리 State를 업데이트
TD > Driving Home Example
 |
 |
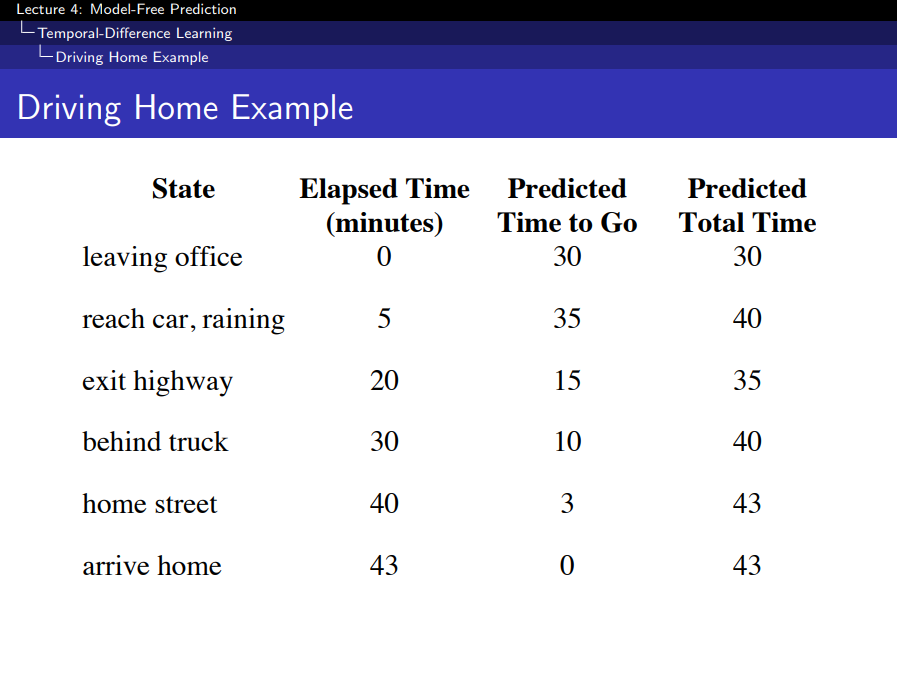
- Elasped Time: 현재 State까지 실제로 총 걸린 시간
- Predicated Time to Go: 예측 걸릴 시간(Like 네비게이션 예측 시간)
- Predicated Total Time: Elasped Time + Predicated Time to Go
- 뒤로 갈 수록 정확해짐
- MC는 종료되고 나서, 모든 State를 최종 Predicated Total Time으로 업데이트해주는 것
- TD는 매 State마다 Predicated Total Time으로 업데이트해주는 것
Advantages and Disadvantages of MC vs. TD (1)
- TD can learn before knowing the final outcome
- TD can learn online after every step
- MC must wait until end of episode before return is known
- MC는 끝날 때까지 기다렸다가 return값을 갖고 업데이트해준다
- TD can learn without the final outcome
- TD can learn from incomplete sequences
- MC can only learn from complete sequences
- TD works in continuing (non-terminating) environments
- MC only works for episodic (terminating) environments
Bias/Variance Trade-Off

- Gt의 기대값 = vπ(St)
- biased estimate of vπ(St)
- Bellman Equation에 의해 증명
- 추측치로 v를 업데이트하기 때문에
- 따라서 Bias 관점에서 TD가 좋지 못함
- Variance 관점에서 TD가 좋음
- 다양한 랜덤 actions, transitions, rewards들에 Return과 TD target이 의존하기 때문에
Advantages and Disadvantages of MC vs. TD (2)
- MC has high variance, zero bias
- Good convergence properties
- (even with function approximation)
- State가 많아지면 테이블에 값을 적을 수 없어서 function approximation을 하는데, 이게 Neural Network
- Not very sensitive to initial value
- Very simple to understand and use
- TD has low variance, some bias
- Usually more efficient than MC
- TD(0) converges to vπ(s)
- (but not always with function approximation)
- More sensitive to initial value
- 초기값을 활용해서 추측치로 v를 업데이트하기 때문
Random Walk Example
 |
 |
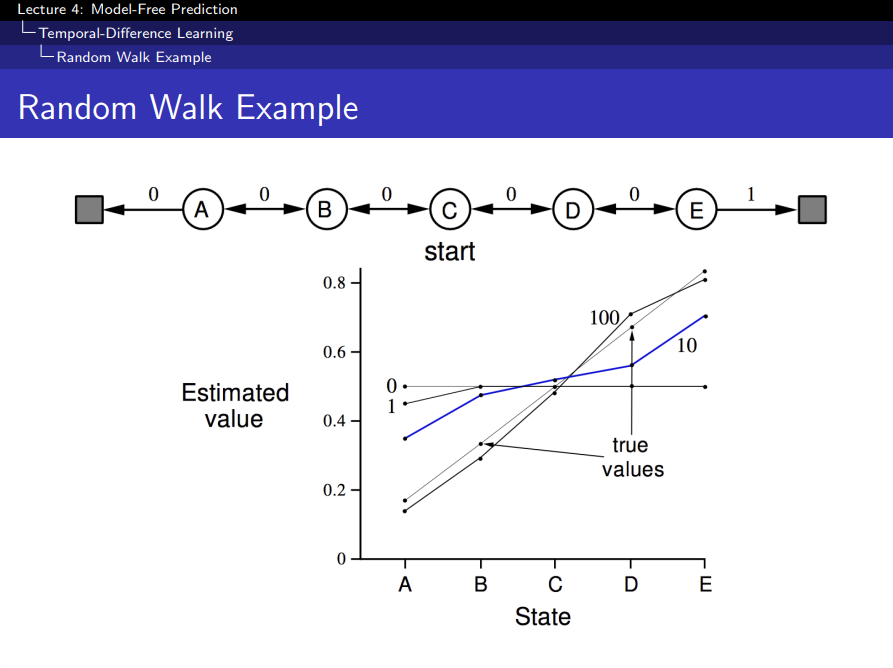
- E쪽으로 끝나면 Reward 1, A쪽으로 끝나면 Reward 0
- 왼쪽 그림
- Epsiode를 0번 학습시켰을 때, 0.5로 초기화해놓음
- TD 방법으로 학습으로 했을 때 100번 Episode에서 수렴을 한다
- 오른쪽 그림
- α에 따라 TD, MC 방법의 결과 그려놓은 것
- Epsiode가 진행될 수록 Root Mean Square Error를 그려놓은 것
- 오류가 늘어나는 이유는 α가 너무 크기 때문임
Batch MC and TD

- Epsiode가 무한할 때, MC와 TD는 V에 수렴
- 제한된 k개의 Episode만 있으면, MC와 TD가 같은 곳에 수렴할까?
AB Example
 |
 |
 |
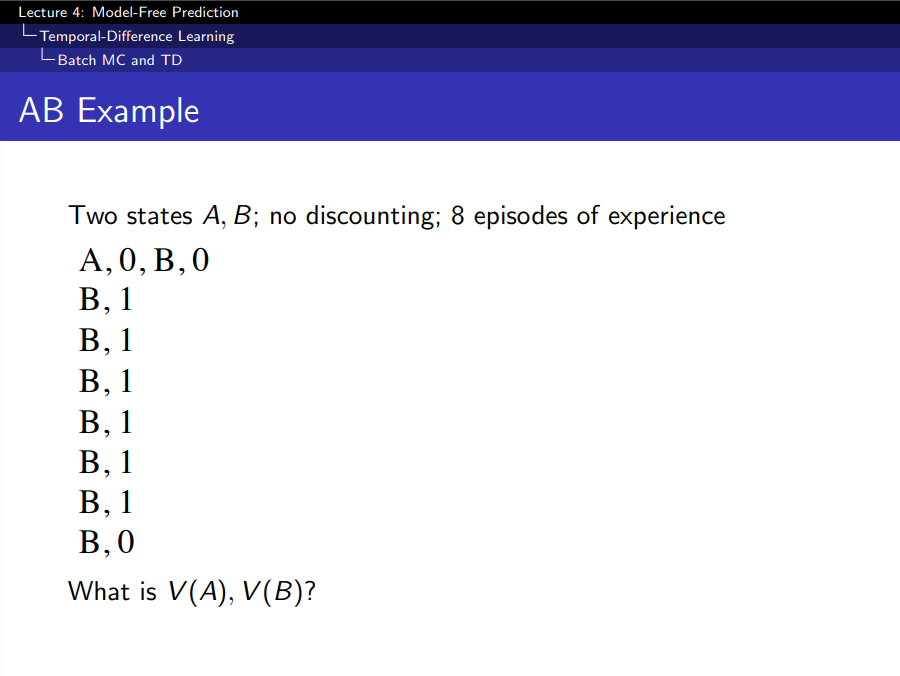
Model-Free이기 때문에 주어진 episode만 있고 model은 모름
- MC를 이용해 V(A) 학습하면, V(A) = 0 = A 방문 수 1, 그때 값 0 → 평균은 0
- TD를 이용해 V(A)를 학습하면, V(A) = 0.75 = 0 + V(B)
Advantages and Disadvantages of MC vs. TD (3)
- TD exploits Markov property
- Usually more efficient in Markov environments
- MC does not exploit Markov property
- Usually more effective in non-Markov environments
- MSE를 minimize함
Bootstrapping: 추측치로 업데이트하는 것. TD Backup은 Bootstrapping한 것
 |
 |
 |
DP: Full-Sweep만 하고, Tree 끝까지 가지 않음 TD(0): 한칸만 가보는 것 TD(1): 두칸 가보는 것 |
Bootstrapping and Sampling
- Bootstrapping: update involves an estimate
- MC does not bootstrap
- DP bootstraps
- TD bootstraps
- Sampling: update samples an expectation (너비 관점에서 본 것)
- MC samples
- DP does not sample: 가능한 모든 action을 다해보기 때문에 sampling하지 않음
- TD samples
Unified View of Reinforcement Learning
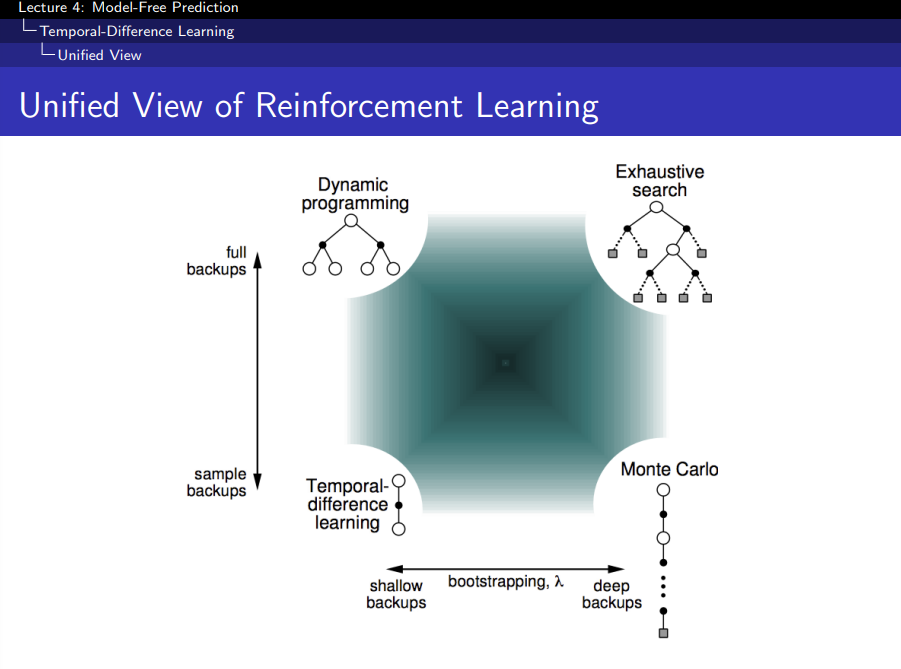
- Exhaustive search: 모든 Tree Node 다 탐색
- Sampling: Agent가 Policy를 따라서 움직는 것
- 즉 Model을 알 때 full backup 가능하나, 모를 때는 sample backup을 수행한다
n-Step Prediction
- 1-step만 가서 bootstrapping할 수 있고
- 2-step까지 간 후, bootstrapping할 수 있음

n-Step Return

Large Random Walk Example
TD(1) ~ TD(1,000)까지의 성능을 분석한 것.

Averaging n-Step Returns

λ-return
- Geometric mean 사용
- Forward-view: 미래를 보는 것
- Backward-view: 과거를 보는 것

TD(λ) Weighting Function
- Geometric mean 사용 이유
- 계산적으로 편함
- Memory-less하게 학습 가능
- TD(0)와 동일한 비용으로 TD(λ) 계산 가능

Forward-view TD(λ)
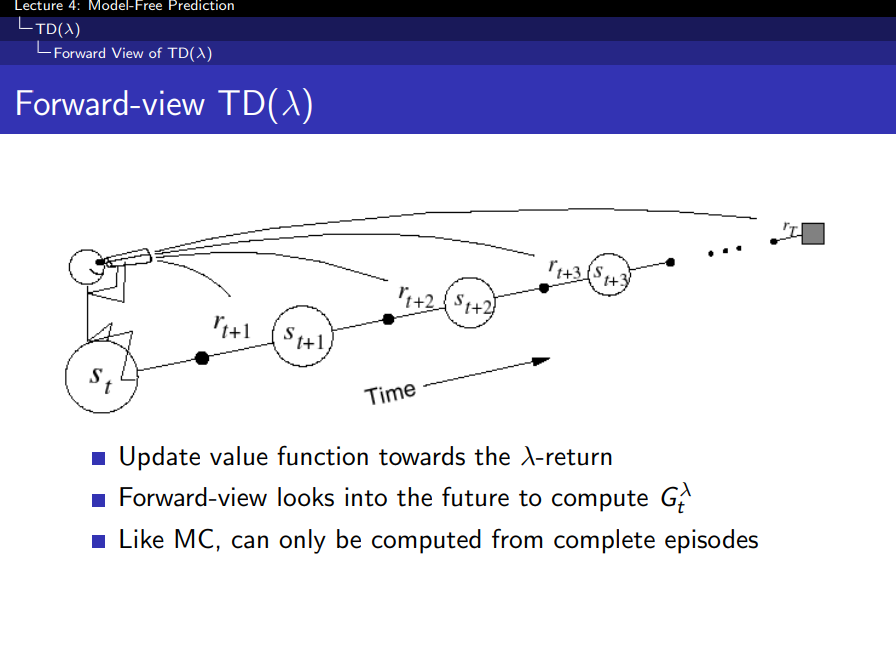
- λ 값에 따라 달라진다
- 미래를 보고 업데이트하는 것. 즉 MC와 동일하게 Episode가 끝나야 업데이트 가능

Backward-view TD(λ)
- Foward-view와 반대로 매 step마다 업데이트 됨
- 각 State마다 업데이트가 발생되면 TD 에러 비율만큼 업데이트를 가중적용함
- 따라서 Episode 길이보다 짧은 기억을 하는 단기 메모리와 같은 역할을 함
 |
 |
Eligibility Traces
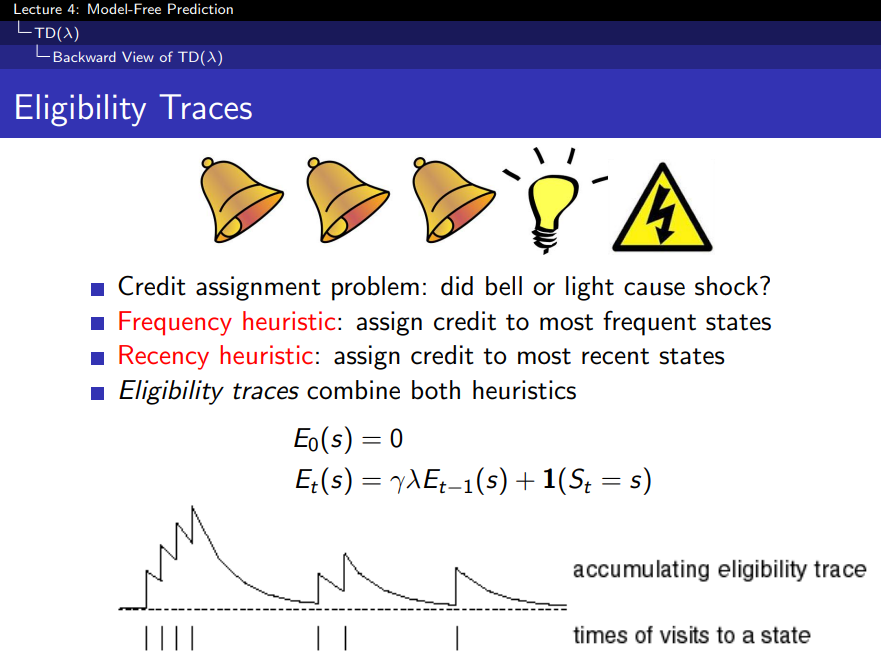
- State 방문하면 1을 올려주고, 방문하지 않을 때마다 γ만큼 줄이기
- 그 값은 1개
- 번개가 다시 발생하는 이유?
- 종 때문인지 전구때문인지 알기 위해선
- 자주 발생한 종이 문제인지, 직전에 발생한 전구가 문제인지를 판단하기 위해서는 두 개 상황을 조합해서 사용할 수 있음
- 즉 Eligibility Traces는 책임사유를 의미함
TD(λ) and MC

TD(λ) and TD(0)
- λ가 0이 되면 가파른 decay가 발생하는데, 이는 현재 State의 Value Function만 업데이트하기 때문에 TD(0)과 동일한 방식이 됨
- λ가 1이 되면 전체 episosde를 커버하고 MC와 동일한 방식이 됨

'Study > Machine Learning' 카테고리의 다른 글
| [RL]Lecture #6 - Value Function Approximation (0) | 2022.03.13 |
|---|---|
| [RL]Lecture #5 - Model-Free Control (0) | 2022.03.10 |
| [RL]Lecture #3 - Planning by Dynamic Programming (0) | 2022.03.06 |
| [RL]Lecture #2 - Markov Decision Processes (0) | 2022.03.06 |
| [RL]Lecture #1 - Introduction to Reinforcement Learning (0) | 2022.03.04 |




댓글